A directed acyclic graph (DAG!) is a directed graph that contains no cycles. A rooted tree is a special kind of DAG and a DAG is a special kind of directed graph. For example, a DAG may be used to represent common subexpressions in an optimising compiler.[1]
Article Language: Chinese
Example Language: Java
Reading Time: 3min
树的性质
对于线性数据结构来说, 元素与元素之间的关系是一对一的. 例如, 在 Linked list 中, 每一个元素只有一个 preceding 和一个 following element. 而对于一对多的情况, 就需要另外一种数据结构树(tree)/图(graph)来处理了. 树是一个特殊的图(DAG). 对于一个非空的树来说, 它是一个拥有 n 个节点(n >= 0) 的有限集合. 这个集合有且只有一个根节点(root), 其他节点可以被看做若干个不相交的子集(n - 1). 而这 n - 1 个子集被视为 root 的子树(subtree). 通过 root 可以访问到它所有的子树[2].
depth: 从节点到 root 的高度.
height: 从 root 到离它最远的节点的距离.
degree: 节点拥有的子树的最大数量.
- 对于一个 tree 中的每一个节点来说, 它的 parent 节点是确定的, 但是 child 节点可以有多个. 对于多个子节点的表示则可以使用 List
这种形式来表示. - 对于每一个节点来说, 它有多少个子树, 就要有多少个 reference 指向这些子树. 那么同样的, 遍历每一个子树的时间复杂度就是子树节点的个数.
- 所以对于一个没有 parent reference 的 tree, 因为只能够通过 root 来遍历/搜索元素, 时间复杂度为 O(n).
- 如果有必要的情况下, 可以增加一个 parent 的域.
- 在遇到复杂的树状结构的时候, 可以使用 child refernce 和 sibling reference 来指向当前节点的子节点和兄弟节点. 这样就可以转化成一个简单的二叉树的结构了.
二叉树
下面来说下特殊的树, 二叉树(binary tree). 二叉树具有五种基本形态, 空树, 只有一个根节点, 根节点只有左子树, 根节点只有右子树, 根节点拥有左右子树. 这个状态适用于每一个节点. 所以对于一个有 3 个节点的树来说, 它应该具有如下几种形态,

有一些形态具有特殊的性质, 这些性质可以帮助我们高效的处理一些数据. 例如,
- 满二叉树(full binary tree): 每一个节点只有两个状态, 没有子树, 或者有两个子树.
- 完美二叉树(perfect binary tree): 除叶子节点外的 node 都拥有 2 个子树, 并且所有的叶子节点都在同一层. 上图中的第一个.
- 完全二叉树(complete binary tree): 任意节点子树之间高度差不超过 1, 也就是说叶子节点只能出现在最下面两层, 如果叶子节点不在同一层, 那么最下一层的叶子节点一定在左边连续位置. 同样的, 如果是倒数第二层的叶子节点, 那么一定在最右边连续位置(其实记住 bubble 在左就够了). 如果一个节点只有一个子树, 那么这个子树一定在左边. 同样节点数的二叉树, 完全二叉树的深度最小. 对于一个拥有 n 个节点的完全二叉树来说, 它的深度是 logn + 1. 若按照层序从 1 ~ n 排列, 对于每一个元素 i(1 <= i <= n), 如果 i == 1, 那么 i 是 root, 如果 i > 1, 它的 parent node 是 i / 2, 如果 2i > n, 则 i 没有左子树( i 为叶子节点). 如果 2i == n, 则 2i 是 i 的左子树. 如果 2i + 1 > n, 则 i 没有右子树. 如果 2i + 1 == n, 那么 2i 是 i 的右子树.
- 平衡二叉树(balanced binary tree): 任意节点子树之间高度差不超过 1.
- 二叉搜索树(binary search tree): 对于任意节点来说, 它所有左子树不能大于它, 所有右子树不能小于它. 中序遍历结果一定是升序.
perfect tree 一定是完全二叉树, 完全二叉树一定是平衡二叉树.
这里 full tree 和 perfect tree 的定义还是有一些争议….
二叉树的遍历
二叉树的遍历( traversing binary tree)是指从 root 出发, 按照某种顺序访问所有节点. 每个节点只被访问一次.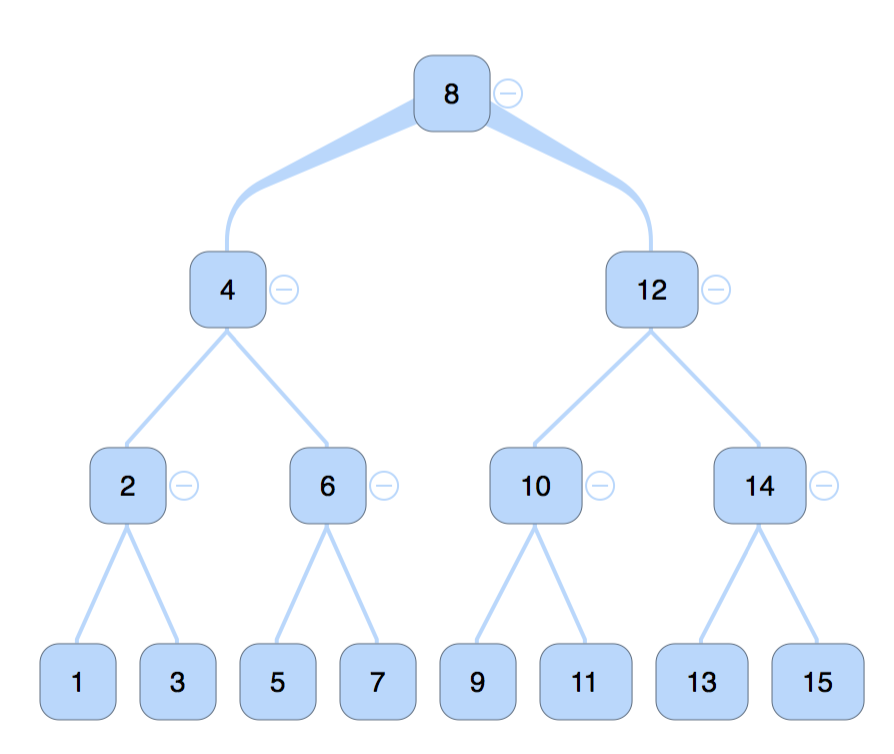
对于一个二叉树来说, 遍历的顺序可以分为深度优先和宽度优先. 根据根节点所在的位置的不同, 深度优先又可以被分为前序, 中序和后序遍历.
- pre-order traverse: 对于每一个节点来说, 先访问它自己, 再访问左子树, 然后访问右子树. 上图结果应该是,
1 | 8 --> 4 --> 2 --> 1 --> 3 --> 6 --> 5 --> 7 --> 12 --> 10 --> 9 --> 11 --> 14 --> 13 --> 15 |
- in-order traverse: 对于每一个节点来说, 先访问左子树, 在访问它自己, 然后访问右子树( root 在中间). 上图结果应该是,
1 | 1 --> 2 --> 3 --> 4 --> 5 --> 6 --> 7 --> 8 --> 9 --> 10 --> 11 --> 12 --> 13 --> 14 --> 15 |
- post-order traverse: 同理, 先左子树, 然后右子树, 最后访问它自己. 上图访问结果,
1 | 1 --> 3 --> 2 --> 5 --> 7 --> 6 --> 4 --> 9 --> 11 --> 10 --> 13 --> 15 --> 14 --> 12 --> 8 |
- level oder traverse: 从上到下, 从左到右分层访问, 通常会用一个 queue 来储存每一层的 TreeNode,
1 | 8 --> 4 --> 12 --> 2 --> 6 --> 10 --> 14 --> 1 --> 3 --> 5 --> 7 --> 9 --> 11 --> 13 --> 15 |
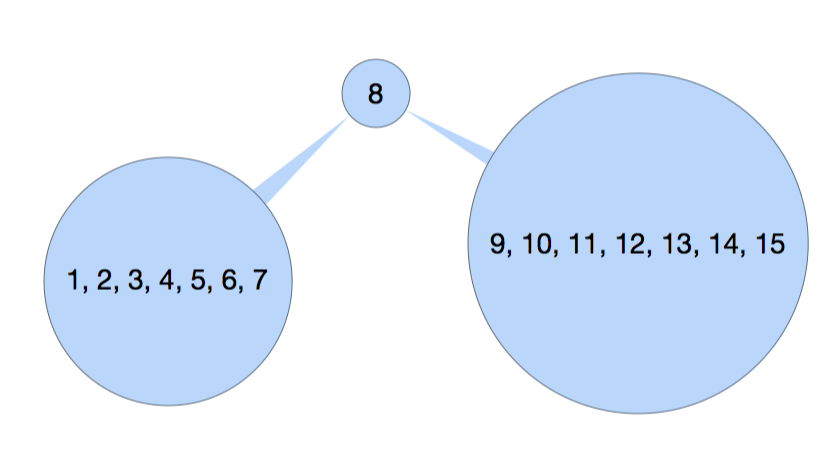
已知前序遍历/后序遍历和中序遍历可以确定唯一一个二叉树, 而知道前序遍历和后续遍历则无法还原一个二叉树的. 这是因为通过前序/后续遍历可以轻而易举的确定 root, 而中序遍历则可以通过这个 root 来确定左右子树的范围. 举例说明上面结果中前序遍历和中序遍历如何还原一个二叉树.
- 已经 pre-order 中, 8 是唯一确定的 root, 那么 in-order 中, 1 ~ 7 则一定是左子树, 9 ~ 12 一定是右子树. 如下,
继续通过 pre-oder 的顺序获取左子树 root,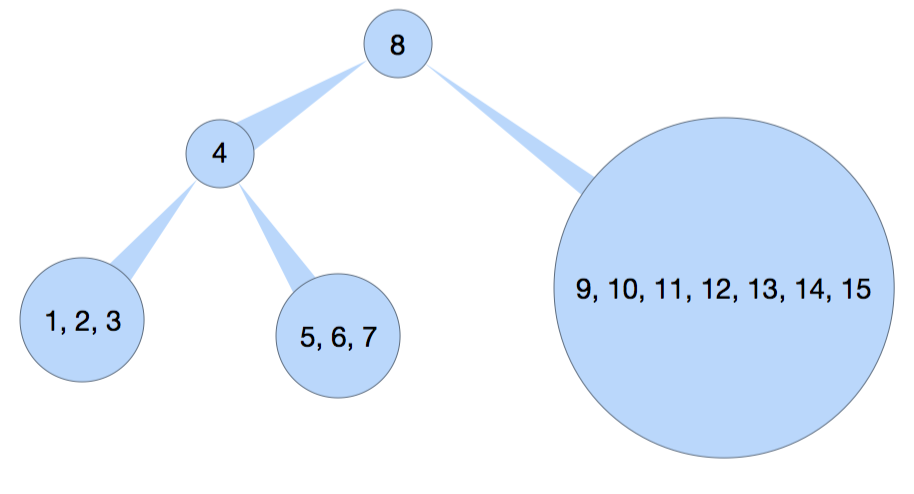
直到最后左右子树元素为 1, 那么确定为叶子节点. 最后再通过同样的逻辑还原右子树.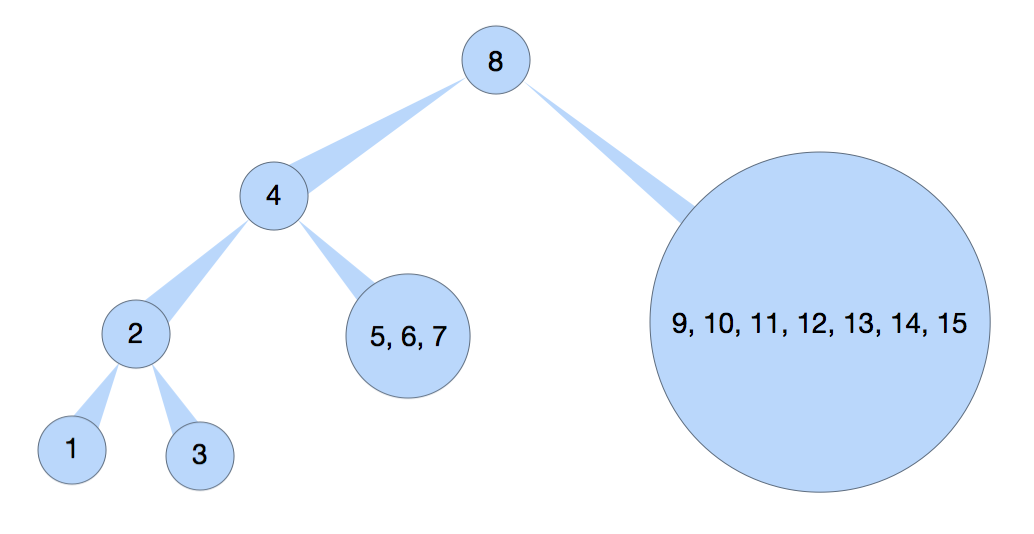
把二叉树以某种顺序线索化(双链表或者 arraylist)的过程叫做序列化, 反之则是反序列化.
[1]: “Directed Acyclic Graphs.” Directed Acyclic Graph (DAG) Algorithms, www.allisons.org/ll/AlgDS/Graph/DAG/.
[2]: 《大话数据结构》 程杰. www.bing.com/cr?IG=31B9721229184349AAEC19BE676BAC6F&CID=362C81AF801A620D0EAF8A7881B563E4&rd=1&h=OJ2Sq1D4wfXY6mddIv_zw1DEo8UFjkz32ZCngLj1biE&v=1&r=https://www.amazon.cn/dp/B0053F0HNW&p=DevEx.LB.1,5871.1.